Initially, composite materials were used only in secondary structures in aviation industry, but as knowledge and development of the materials has improved, their use in primary structures such as wings and fuselages has increased (Fig. 1). Nevertheless, the behaviour of high-performance laminar and fibrous composite materials with interfacial defects, which triggers fracture, is still not sufficient known. This fact emphasises the importance and the necessity of current studies.
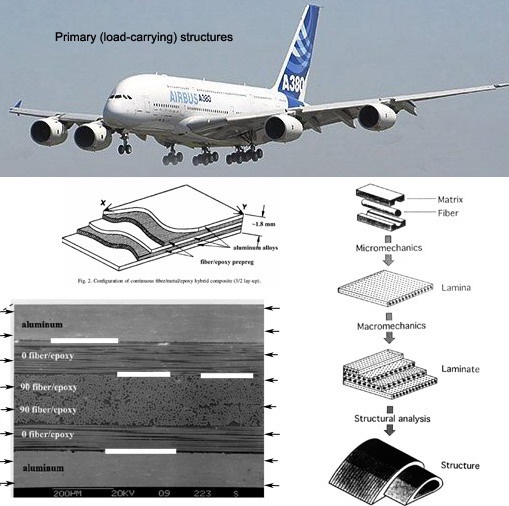
Figure 1. Cross-section of carbon-fibre aluminium laminate, a part of primary structure of Airbus A380
Understanding of fracture due to specific mechanisms inherent to heterogeneous materials will play an increasingly significant role. This function will expand not only as a result of improved material performance, but also as human ingenuity finds more and diverse areas where composite materials can be beneficially employed and leveraged.
A good understanding of the compression failure mechanisms, specific only to heterogeneous materials, is crucial to the development of improved composite materials. The compressive strength of composites is generally lower than the tensile strength by about 2/3. Therefore, this relative weakness in compression is often the limiting factor in the application of composite materials. In order to design a composite structure to operate efficiently and safely under compressive loading, it is necessary to be able to accurately predict the compressive strength of that structure, taking into account the possible failure modes of the structure under different conditions.
Composite material structures were generally considered as two-dimensional laminates, on a structural level, laminated components such as beams, plates and shells are analysed for global stability in compressive environments by extending classical beam, plate and shell theories for isotropic materials to laminated structures via classical lamination theory. Buckling prediction results for thin laminates (usually less than 36-48 plies) generated using classical lamination theory are generally good. Predictions for thick laminates based on classical lamination theory have not been very realistic. All of the above theories treat the laminate as an equivalent anisotropic medium (a direct implication of the use of classical lamination theory type theories) and therefore, cannot predict any internal material breakdown.
The most accurate approach to study mechanical behaviour of composite materials is based on piecewise-homogenous medium model and three-dimensional theory of deformable bodies' stability. This approach considers full-field stress state and accounts for the internal structure of composite, thus existence of internal defects, delaminations, etc.
Recently, there is a large amount of studies devoted to the stability and fracture problems of composites in compression. In the most of studies it is assumed that defectless structural elements of the material are rigidly attached, thus the continuity conditions of stresses and displacements vectors are satisfied at interfaces. However, experimental studies proved that this assumption is far away from reality. Intralaminar defects and various cases of interfacial adhesion reduction may occur in real composites such as delaminations, debonding, cleavages, slippage zones and cracks due the fabrication process or operating condition. Therefore, in these cases the assumption of continuity of stresses and displacements vectors is no longer valid, thus it is important to incorporate into analysis the real structure of composite materials.
The main objective of this project is to investigate the effect of interfacial cracks interaction on the critical buckling strain in layered and fibrous composite materials under compressive static loading. These studies involve parameterised variables, such as the crack size, the crack spacing, the layer volume fraction and the fibre volume fraction. Furthermore these parametric studies are conducted for two types of cracks, namely cracks with stress-free crack faces and cracks with frictionless Hertzian contact of the crack faces.
In the first case an interaction of the crack faces is not taken into account and interpenetration of the crack faces is allowed. This is so called 'classic crack' model. In the second case, when formulating boundary condition on the crack surfaces the following two possible cases are taken into consideration: (i) the modes of stability loss with an 'open' shape for the cracks are analysed, and (ii) the shear-type modes of stability loss are studied, where the possible closing of crack surfaces and their interaction is investigated.
The following assumptions are adopted: (i) the onset of fracture process coincides with local loss of stability of the equilibrium state of the material that surrounds the crack; (ii) the critical strain corresponding to loss of stability in the microstructure of the composite, either surface or internal instability, must be smaller then the critical strain corresponding to loss of stability of the entire composite.
The multi-scale modelling methodology of composite material system is adopted, where depending on the hierarchy of structural scale of studied phenomena, the modelling ranges from a series of plies (Fig. 2) down to single fibre (Fig. 3). An emphasis has been placed on application of the model of piecewise-homogeneous medium and the three-dimensional theory of deformable bodies' stability, the most accurate approach to study a mechanical response of solids. The mechanical behaviour of each composite constituent is described by three-dimensional linearised equations of solid mechanics, provided certain boundary conditions are satisfied at the interfaces.
Furthermore, the Finite Element Analysis, using the linear elastic eigenvalue extraction method, has been applied to investigate the effect of interfacial cracks interaction on the critical strain.
Finally, the post-processing analysis has been performed to determine the characteristic parameters of interfacial crack interaction phenomena.
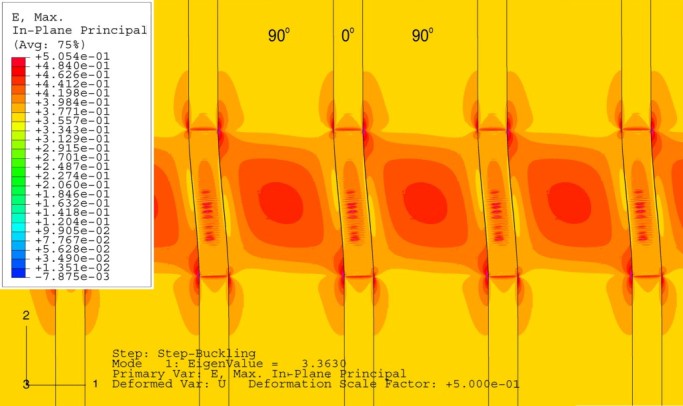
Figure 2. FEA result for the shear mode for a graphite-epoxy composite model with frictionless Hertzian contact interaction of the crack faces. Colour map shows maximum in-plane principal strain distribution for, crack size a/h = 5, cracks spacing b/a = 0, 0°-plies volume fraction V0 = 0.2

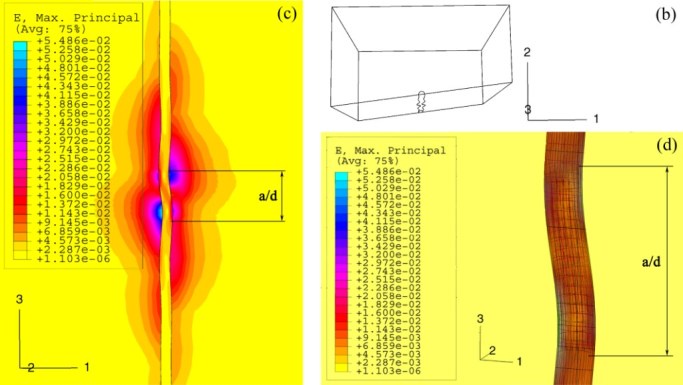
Figure 3. FEA results for carbon fibre in epoxy resin matrix and for the 'classic' crack model; the crack size a/d = 5; the critical strain is 6.15 %. (a) RVE shows buckling pattern and the maximum in-plane principal strain distribution on the fibre/matrix interface; (b) The cross-section shows the fibre buckling plane; (c) The maximum in-plane principal strain distribution on the cross-section shown in Fig. (b); (d) the buckling pattern in the vicinity of a crack
Related publications:
-
Winiarski B, Guz IA. The effect of cracks interaction in orthotropic layered materials under compressive loading. The Philosophical Transactions of the Royal Society A. 2008, 366(1871), pp.1841-1847.
-
Winiarski B, Guz IA. The effect of fibre volume fraction on the onset of fracture in laminar materials with an array of coplanar interface cracks. Composite Science and Technology. 2008, 68(12), pp.2367-2375.
-
Winiarski B., Guz I.A. The effect of cracks interaction for transversely isotropic layered material under compressive loading. Finite Elements in Analysis and Design. 2008, 44(4), pp.197-213.
-
Winiarski B, Guz IA. Plane problem for layered composites with periodic array of interfacial cracks under compressive static loading.International Journal of Fracture. 2007, 144(2), pp.113-119.
-
Winiarski B, Guz IA. The effect of crack faces contact interaction on the critical strain in composites under compressive loading. PAMM - Proceedings in Applied Mathematics and Mechanics. 2007, 7(1), pp.4030001-4030002.
