Applied Mathematics

Formally, nonlinear dynamics refers to the behaviour of systems where changes in inputs are not proportional to changes in output. In practice, this means the system usually contains feedbacks and relationships between quantities that can lead to complex and unpredictable behaviour. Nonlinearities are present in many natural and mathematical systems. Much of our theoretical work in this area is to identify mathematical structures and patterns that describe real nonlinear systems.

Chaotic systems are a subset of nonlinear systems. Their main characteristic is that small uncertainties in initial states grow exponentially fast, making practical prediction impossible after some time. Such systems appear to behave randomly but in fact do not.

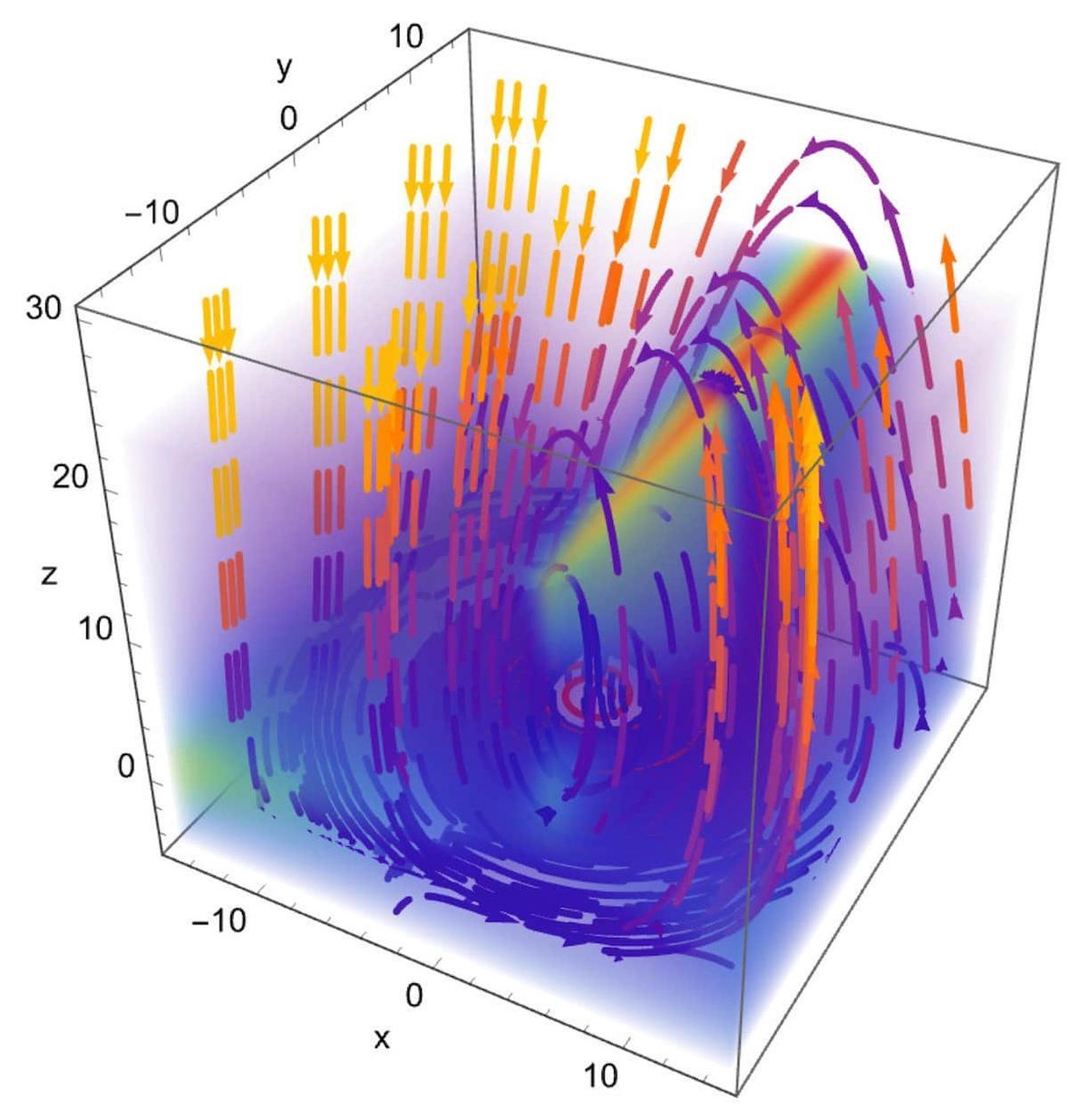
We have many staff working in the fields of nonlinear dynamics and chaos. Much of the department’s work in nonlinear dynamics is related to biological systems. This is organised under the umbrella of the interdisciplinary Institute for Complex Systems and Mathematical Biology (ICSMB), which was founded in 2009.

Right, top: Angular speed diagnostics in the Rossler system showing phase speeds and phase space streamlines. From Thiel (2024).

Among the techniques we employ, nonlinear time series analysis is one of the most widely used. We use this to analyse, classify, and predict the dynamics of real-world data. This requires addressing noise, uneven sampling, and missing variables. Often the full dynamics of a system of coupled differential equations can be reconstructed from the dynamics of a single observed quantity.

Right, middle: Phase diagram showing a logistic-tent map with no equilibria, and the bifurcation diagram for this system, varying the height of the tent map. From Lawnik et al. (2024).

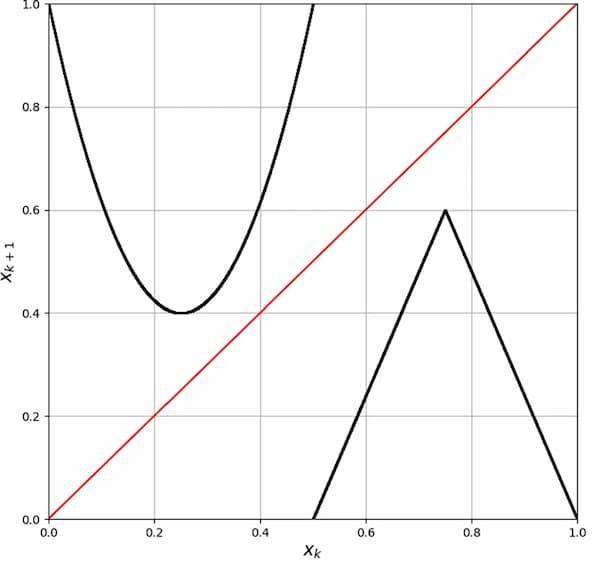
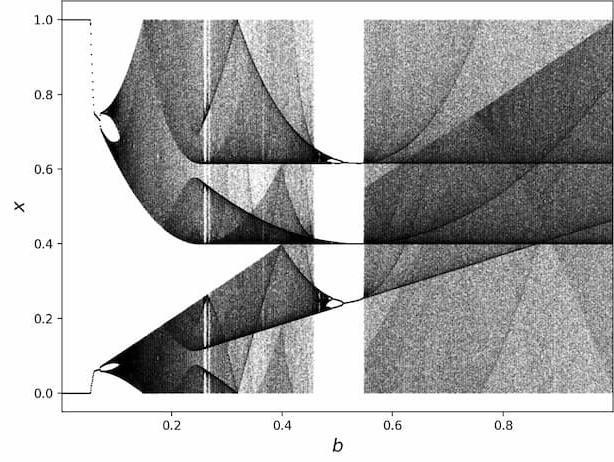
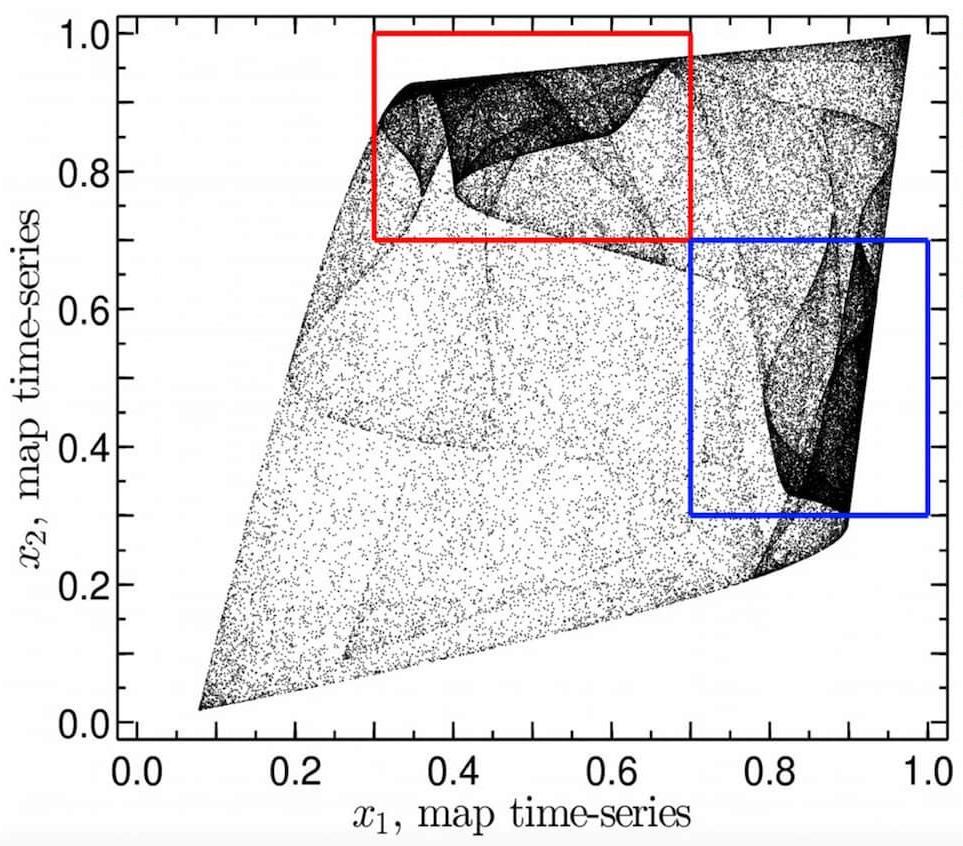
We study a wide and ever-evolving set of topics in nonlinear dynamics. For individual staff members’ interests, see the bottom of this page. Examples include:

• Stellar astronomy
• Ecology
• Critical patient care
• Psychiatry
• ECG analysis
• Geophysical fluid dynamics
• Genetic networks
• Neural network dynamics
• Transient chaos
• Chaotic advection of fluid flows
• Protein translation and synthesis
• Recurrences
• Coupling between transcription and translation
• Ribosome synthesis
• The cell cycle
• Combinatorial stresses in yeast
• Epilepsy
• Population dynamics
• Traffic flow
• Fractal geometry
• Social and infrastructure systems links to disasters
• Transformations that preserve chaos
• Maps without equilibria
• Spatio-temporal nature of causality 
• Social and infrastructure links to disasters

Right, bottom: Attractor for two coupled heterogeneous logistic maps with a = 3.9 and a = 4.0. From Rubido, Grebogi, and Baptista (2018).

Staff contacts: Celso Grebogi, Murilo Baptista, Sandip George, Nicolas Rubido, Alessandro Moura, Ekkehard Ullner, Francisco Perez-Reche, M. Carmen Romano, Bjoern Schelter, Kapil Debnath, Claudiu Giuraniuc, Marco Thiel, Roland Young.

In complex systems, many interacting parts combine to influence the behaviour of the whole. Network theory concerns the relationships between different parts of a complex system. Emergent phenomena are behaviours that emerge on a system-wide scale from the interactions between individual elements of a system.

Major subfields include synchronisation of individual elements of a complex system, and phase transitions, where the behaviour of the whole system changes in response to changes in external forcing.

We aim to explain and predict the collective behaviours that can emerge - such as chaos or synchronisation - from the network of connections between a system’s components. We are also interested in reverse engineering a system's connectivity from observations of its collective behaviours.

Since networks and emergent phenomena appear in many disciplines, we collaborate on various inter-disciplinary topics. Examples of specific topics we study in this area include:

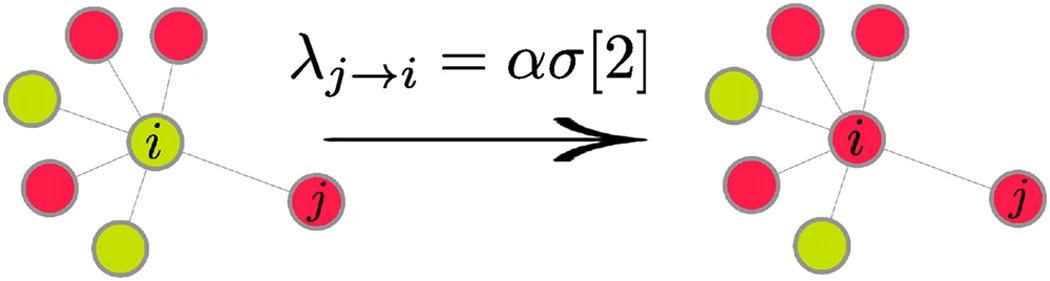
• Brain network studies (including Alzheimer's disease, depression, ageing, and multiplex neuronal networks)
• The sleep-wake cycle of mammals (studying consciousness and its alterations)
• Climate change and forecasting at intra-seasonal timescales
• Stability of power-grid systems
• Infectious disease
• Social contagion (going "viral")

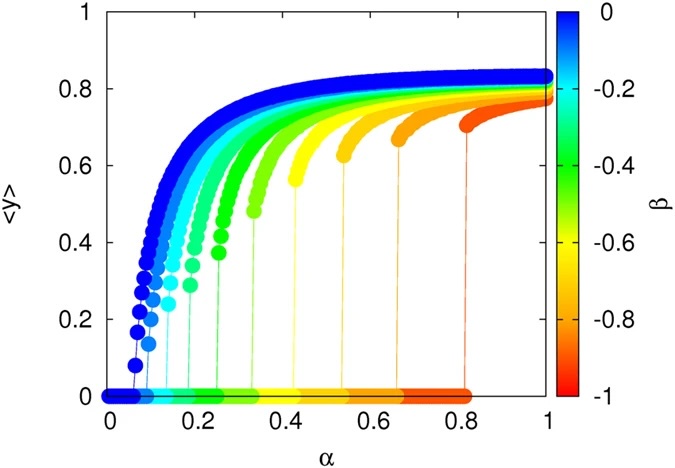
Right: (Top) Schematic showing a model of transmission in a susceptible-infected-susceptible epidemic model with a synergistic rate based on the number of healthy individuals connected to a receiver. (Bottom) Resulting concentration of spreaders in the steady state as a function of transmission rate α and synergistic parameter β. From Gómes-Gardeñes et al. (2016).

Staff contacts: Nicolas Rubido, Francisco Perez-Reche, Murilo Baptista, Marco Thiel, Claudiu Giuraniuc, Celso Grebogi, Ekkehard Ullner.

The general approach of transforming a real-world problem into a series of logical steps written down in abstract mathematical language (often as differential equations) underpins much of the research across our department. It can be applied to almost any field of study. Mathematical models capture the essential dynamics and behaviour of a system, providing insight into both theoretical constructs and real-world phenomena.

We collaborate extensively with researchers across diverse disciplines, offering mathematical modelling expertise to solve applied problems in fields ranging from neuroscience, finance, and molecular biology to environmental science, forensic analysis, and epidemiology. We engage with industrial partners in the oil, health, and whisky industries, applying mathematical frameworks to optimize processes and analyze data-driven challenges.

Some specific models and types of model that we have expertise in include:

• Climate models (MITgcm, Mars PCM)
• Stochastic models (to study synthetic genetic oscillators, neuronal networks, transcription, chromatin, nucleosome chaperoning, and metabolic cycling)
• Plasma models (HPEM, nonPDPSIM, MCFPM)
• Source attribution (MMD)
• Epidemiological models (Explosive Immunization)
• Statistical models (Biochar Engineering)
• Machine learning models (ESPClust, Water Risk Analysis)

We have significant expertise and experience applying Wolfram Mathematica to research problems, and it is also used throughout our MSc Data Science program.

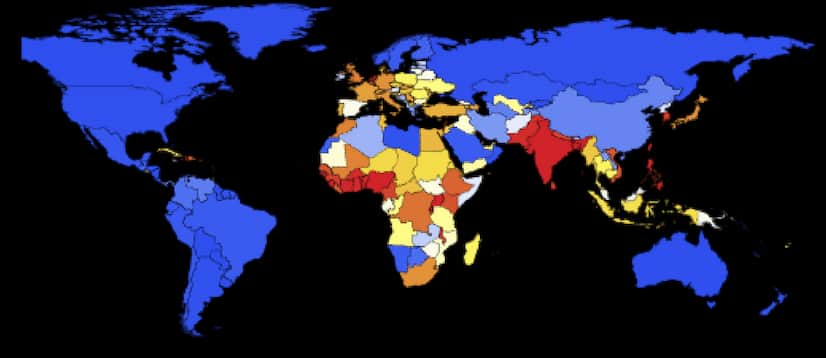
Right: A model simulating a global Ebola epidemic showing the number of deaths at an early stage of the simulation. From Kaurov & Thiel (2014).

Staff contacts: Marco Thiel, Roland Young, Scott Doyle, Murilo Baptista, Francisco Perez-Reche, Nicolas Rubido, Claudiu Giuraniuc, Ekkehard Ullner, Alessandro Moura, Andrew Angel, Sandip George, M. Carmen Romano, Bjoern Schelter.

Mathematical physics concerns the development of mathematical techniques to tackle problems in physics.

At Aberdeen, we are at the forefront of the emerging interdisciplinary field of relativistic quantum chaos. Quantum chaos is the study of quantum manifestations or fingerprints of chaotic behaviour in corresponding classical systems, an interdisciplinary field that has been active for more than three decades. Early research was on non-relativistic quantum systems described by the Schrödinger equation.

Recent years have witnessed a rapid growth of interest in Dirac materials such as graphene, topological insulators, molybdenum disulphide, and topological Dirac semimetals. Their physics is governed by the Dirac equation in relativistic quantum mechanics, generating phenomena that are not usually seen in conventional semiconductor materials.

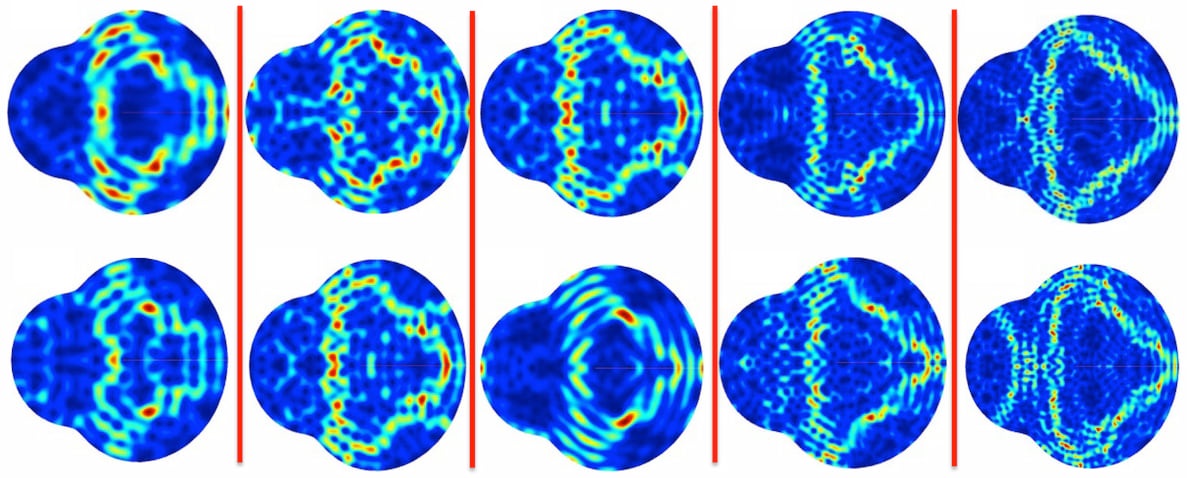
As a result, the new field of relativistic quantum chaos has appeared, which aims to uncover, understand, and exploit relativistic quantum manifestations of classical chaos. At the ICSMB we have pioneered and are at the forefront of this emerging interdisciplinary field, which brings together concepts from the three major revolutions in twentieth century physics: relativity, quantum mechanics, and chaos. 

We are also interested in differential geometry, Clifford algebras, and the Cosserat theory of rods.

Above: Examples of relativistic quantum chiral scars in a chaotic Dirac billiard system. From Lai et al. (2018).

Staff contacts: Celso Grebogi, Charles Wang.

Communication with chaos is a diverse area with links to encryption, engineering, and information theory. By using the unpredictable properties of chaos, we can encrypt signals in a pseudo-random way, but because chaos is fundamentally non-random, we can use the same chaotic properties to decrypt such a signal. This can be used to improve the security of communication systems.

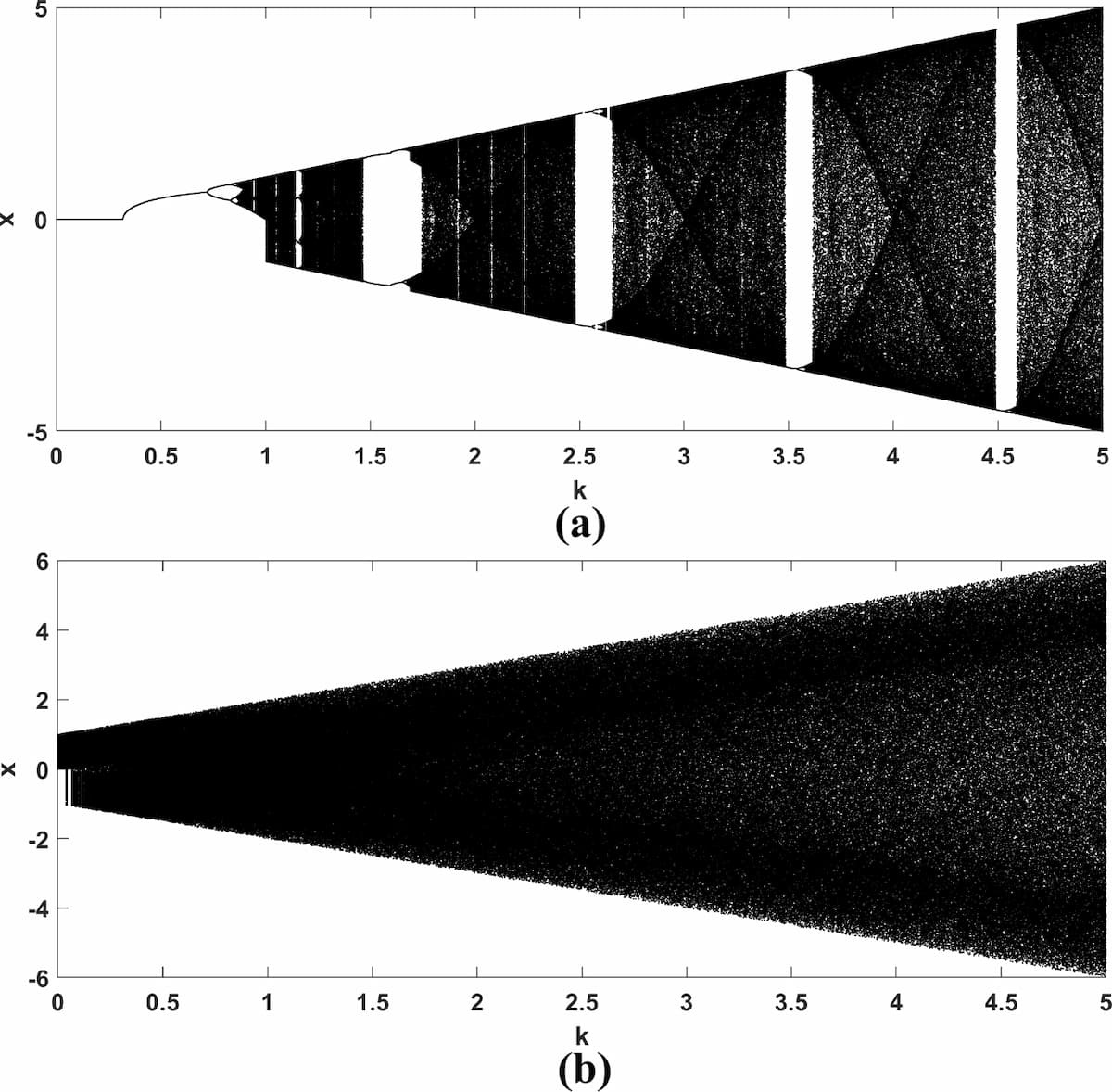
Right, top: Bifurcation diagrams of the sine map and its modified map after chaotification. From Moysis et al. (2025). Increasing the amount of chaos in systems like this can be used to improve the randomness of an encryption key. 

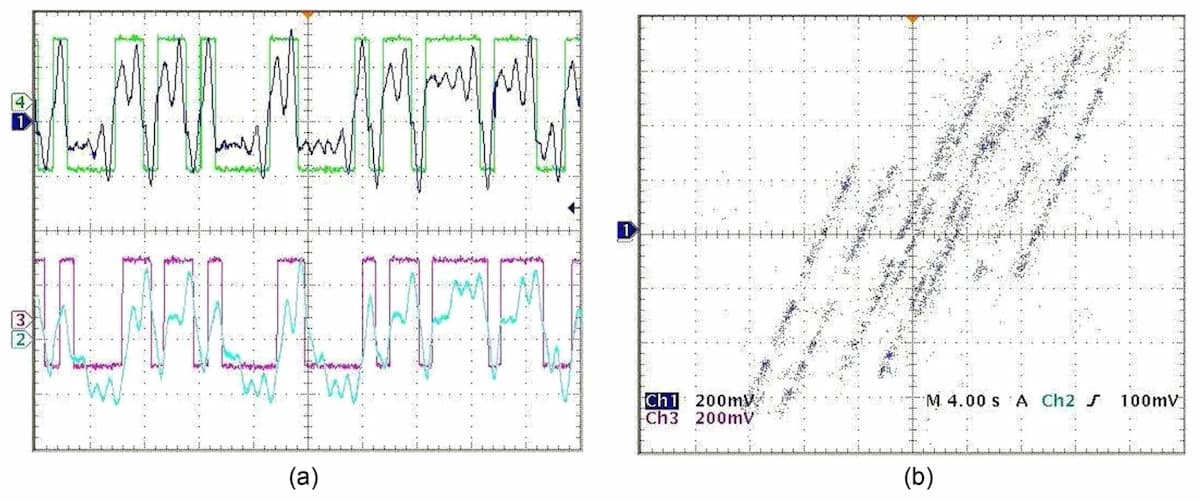
Our research is leading in chaos-based communication. We work to show that chaos offers alternative technologies for efficient, smart, and secure wireless communication systems in the air and in space.

Right, bottom: Experimental validation of wireless communication with chaos, showing the transmitted and filter output signals, and the return map after being transmitted over a wireless channel with three paths. From Ren et al. (2016).

Staff contacts: Murilo Baptista, Kapil Debnath, Celso Grebogi, Ekkehard Ullner.