My thanks to Prof Michael Beaney (Regius Chair of Logic, University of Aberdeen) and Prof Gavin McLeod Little (University of Stirling) for thoughtful review and discussion of these ideas, and to seminar students on University of Aberdeen, School of Law’s UK Constitutional Law module, who helped to spark my thoughts in the first place over the course of our “Seminar 1” discussions on Parliamentary Sovereignty.
The UK Constitutional Law Association recently published a short article I wrote on its Blog, entitled Russell’s Paradox and the Principle of Parliamentary Sovereignty. The article drew on a particular intellectual tradition within philosophical logic as a means of demonstrating that an influential definition of the UK’s doctrine of “Parliamentary Sovereignty” stated by A.V. Dicey was logically fallacious.
In the present article I provide a less truncated version of the original article, elaborate on certain matters in an expanded or additional fashion, and most importantly develop the conclusions beyond those offered in the in the original (which appeared under the heading “Further Thoughts”). I do this by adding a supplementary section that further develops the solutions on logical grounds that were offered in the original conclusions.
For the original article, please see: T. L. Muinzer, “Russell’s Paradox and the Principle of Parliamentary Sovereignty”, U.K. Const. L. Blog (23rd April 2021)
Background
The Brexit process has served to draw significant attention to a rich variety of questions engaging the character and scope of the doctrine of Parliamentary Sovereignty, see e.g.: Professor Mike Gordon, with reference to the European Union (Withdrawal Agreement) Bill and the implementation of the EU Withdrawal Agreement (part 1 and part 2); Professor David Feldman, with reference to R. (Miller) v. Secretary of State [2016] and issues arising therein.
In this brief discussion, I do not propose to re-tread this sort of erudite and valuable ground. Rather, I seek to disconnect the doctrine of Parliamentary Sovereignty from typical legalistic discussion and consideration, situating it instead in the context of a particular philosophical method arising in the history and discipline of philosophical logic, prominently embodied by “Russell’s Paradox”. It will be seen that this approach provides a novel perspective, and that it underscores a degree of logical inconsistency underlying the classic Diceyan conception of Parliamentary Sovereignty.
Dicey and Parliamentary Sovereignty
The principle of Parliamentary Sovereignty is typically considered to be a foundational component of the UK’s uncodified constitution. The most influential statement on Parliamentary Sovereignty as an abstract concept is provided by AV Dicey in The Law of the Constitution (1885). Endeavouring to reduce things to their essentials, Dicey summarises as follows:
The principle of Parliamentary sovereignty means neither more nor less than this, namely, that Parliament… has, under the English constitution, the right to make or unmake any law whatever; and, further, that no person or body is recognised by the law of England as having a right to override or set aside the legislation of Parliament.
If this influential definition is disconnected from traditional legal debates and commentary, and is situated instead in isolation within the context of the Russellian intellectual tradition alluded to above, an interesting perspective arises. Indeed, in my view, this type of “thought experiment” goes so far as to offer a logical proof in its own right that the conception fails to hold.
For present purposes, it is sufficient to isolate the following component of Dicey’s conception: UK Parliament has “the right to make or unmake any law whatever”. Before proceeding, I must say a little about Russell’s Paradox and so-called “set theory”.
Russell’s Paradox
In the early 20th Century, distinguished British Philosopher Bertrand Russell (1872–1970) wrote to German logician and philosopher Gottlob Frege (1848–1925), pointing out that certain hitherto undetected paradoxes arose in work Frege was doing in the area of logic. Russell’s observations became known in philosophy as “Russell’s Paradox”. Russell’s Paradox involves sets. Sets are a collection of things that share some sort of common property. For example, the set of all even whole numbers under 10 is: {2, 4, 6, 8}. The set of all odd whole numbers under 10 is: {1, 3, 5, 7, 9}.
Put in simple terms, Russell pointed out to Frege the following. In considering it, let us first bear in mind that there are, of course, “sets of sets”. For example, if a set that we call, say, X, is a set that contains the sets of all odd and even whole numbers under 10, we can assume with confidence that X will include amongst its contents both the set of all even whole numbers under 10 noted above, and the set of all odd whole numbers under 10 noted above. Russell pointed out as follows. Let us suppose that R indicates the set of all sets that are not members of themselves. Russell queried whether this set, R, could be a member of itself. If it is a member of itself, then it satisfies the condition of being excluded as a member of itself. Conversely, if it is not a member of itself, then it satisfies the condition of being included as a member of itself. Here, a paradox appears to arise - Russell’s Paradox.
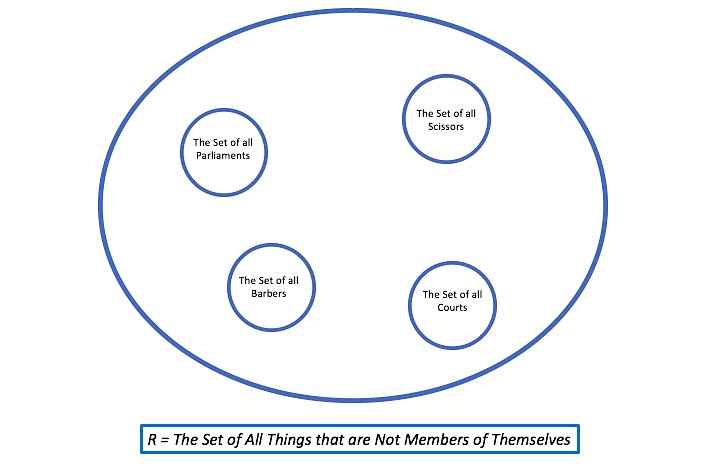
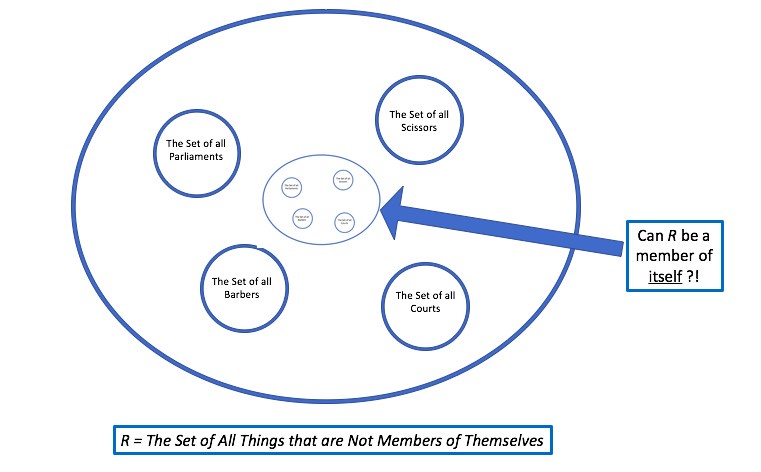
The general type of problem arising here can be demonstrated usefully by way of example. Take a village barber. Let us say that he works in a village where all the men shave, and where the barber shaves all the men in the village that do not shave themselves. Let us further stipulate that these are the only men that the barber shaves. As Russell summarises it in The Philosophy of Logical Atomism, “You can define the barber as ‘one who shaves all those, and those only, who do not shave themselves’” (p.101 of the 2010 Routledge Classics edition). But problems arise if we then pose this question: does the barber shave himself? If we conclude that the barber shaves himself, we seem compelled to place him in the category (i.e., the set) of those who do not shave themselves, because we know that the barber shaves only those who do not shave themselves. If he does not shave himself, we seem compelled to place him in the category of those who are shaved by the barber, because those who do not shave themselves are shaved by the barber, i.e., himself. As Quine puts it, therefore, “We are in trouble if we say the barber shaves himself and we are in trouble if we say he does not.” A paradox has arisen.

Making and Unmaking any Law Whatever
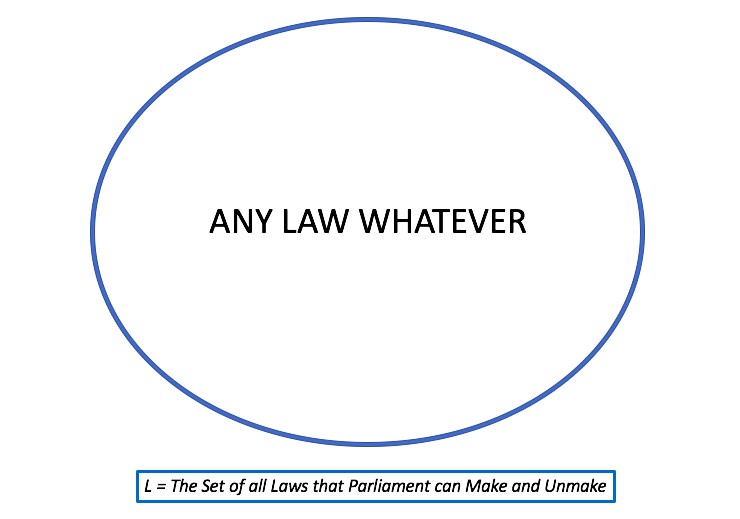
Returning now to Dicey, and the proposition that Parliament can make and unmake any law whatever, this statement suggests on logical grounds that a set may be said to exist that represents the laws that Parliament can make and unmake. I will call this set L (for “Law”). Contained within this set is “any law whatever”. Thus, the set L embodies the totality of laws that national Parliament has the capacity to make and unmake. In summary:
- Parliament can make and unmake any law whatever
- L = the laws that Parliament can make and unmake
- Thus the following set can be expressed: L { any law whatever }
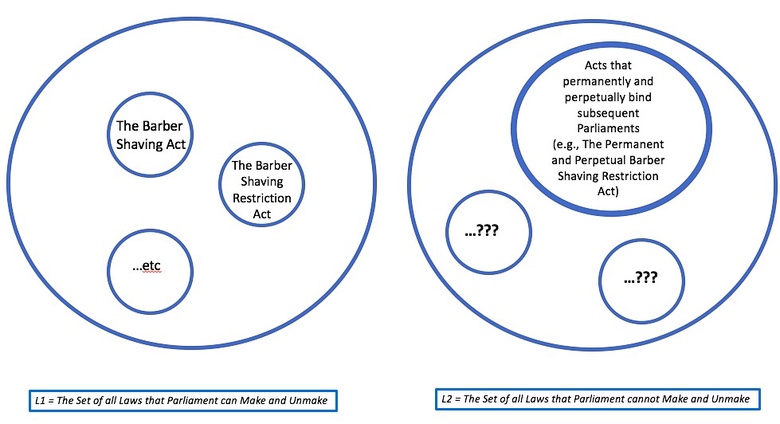
But there is a problem here. Initially, one runs into no difficulty where one considers a conventional sort of Parliamentary law and seeks to situate it within set L. For example, national Parliament can pass a Barber Shaving Act that asserts that all barbers must undertake a specified degree of formal training and achieve a practice certificate in order to be permitted to shave men in the UK. Similarly, a Barber Shaving Restriction Act can be passed, asserting that no barbers are permitted to shave men in the UK. These examples fall squarely within the set L.
It is possible, however, to conceive of a decidedly more problematic sort of Parliamentary law. For example, let us take the hypothetical Perpetual and Permanent Barber Shaving Restriction Act. Let us assume that this Act contains only one section, which reads as follows:
All barbers in the UK are perpetually forbidden from shaving men, and national Parliament can never repeal or otherwise unmake this permanent law.
Parliament can make any law, and thus it can make the Permanent and Perpetual Barber Shaving Restriction Act, such that this Act falls within the set L. However, the Act is a law that constrains Parliament from unmaking it. Thus, simultaneously, the Act cannot be placed within the set L, because L is also the set of all laws that Parliament can unmake, and Parliament is precluded from unmaking this law. The Act thus sits outwith the purview of L on these grounds.
Here, to borrow Quine’s words from above, we are in trouble again. The conclusion on grounds of logic is that the dictate contained within the Diceyan statement of Parliamentary Sovereignty that we have isolated, which asserts that Parliament can make and unmake any law whatever, is in fact a paradox that is not logically sustainable. The assertion is therefore logically inconsistent, and thus fallacious.
Further Thoughts
This isolated thought experiment indicates that the classic Diceyean conception of Parliamentary Sovereignty, at least as expressed in the reductive summative quotation considered above, is inconsistent and thus fallacious. This suggests that it requires to be reframed in a logically coherent manner.
Helpful reframing for the legal mind of the logically inconsistent Diceyan L category can be achieved, it appears, by framing it as two sets, as follows. Firstly: the set of laws that national Parliament can make and unmake, which I will call set L1. Secondly: the set of laws that national Parliament cannot make and unmake, which I will call set L2.
In the isolated philosophic context of this thought experiment, a logically coherent contribution to knowledge can be achieved by taking the general rule that “Parliament can make and unmake any law whatever”, and calculating the latent categories of exceptions to the rule that exist. These categories of exceptions can be inputted into set L2, in addition to the category that I have already inputted, which has been generated by the discussion above.
After the original version of this article was published by the UK Constitutional Law Association, Michael Detmold wrote in a comment on the piece as follows:
If Parliament legislates: ‘all must do X, and all must not do X’ the legislation is null, not because any prior, or currently invented, constitutional state of affairs makes it null: it is null because it is null. …My case about X is the simplest one because of its complete contradiction; but there are many more logical problems than straight contradiction, and one of them is Russell’s paradox.
Here, then, Prof Detmold points to another L2 category that can be inputted into the diagram above: laws that are logically inconsistent and thus ‘null’ (to use his word) due to internal contradiction.
Sets Development
The analysis above diagnoses certain problems inherent in aspects of Dicey’s influential commentary on Parliamentary Sovereignty and posits a basic L1 / L2 logical framing as an improved development intended to appeal to and assist the conventional lawyerly mind. In terms of traditional Russellian logic, however, it is possible to refine this treatment for superior logical accuracy.
Here, working from our Diceyan statement that UK Parliament has “the right to make or unmake any law whatever”, one can approach the problems flagged above by recasting the solution to distinguish and separate out the set of laws that Parliament can make, and the set of laws that Parliament can unmake. I will call the set of laws that Parliament can make S1 (for “Set 1”), and the set of laws that Parliament can unmake S2 (for “Set 2”).
As to the Diceyan S1 category, containing the laws that Parliament can make, it appears that a set like this cannot contain “all laws”, because the discussion has clarified that Parliament cannot make a law that cannot be unmade, such as our Perpetual and Permanent Barber Shaving Restriction Act.
As to S2, however, this category is different in character and less problematic. S2 contains the laws that Parliament can unmake. The reason that this set is somewhat more straightforward than S1 is, is that where one asserts that Parliament can unmake a law, there is a presupposed assumption that the law can indeed be made. Put another way, the Diceyan S2 category carries the assumption that Parliament can unmake any law it can make. This seems unproblematic.
The L1 set that I introduced under the “Further Thinking” heading above in order to assist lawyers in re-framing the Diceyan thinking at issue in a logically coherent manner was defined as “The set of all laws that Parliament can make and unmake”. Where L1 is woven into our more philosophically refined S1 and S2 thinking here, it constitutes the intersection of S1 and S2. I convey this in the following diagram:
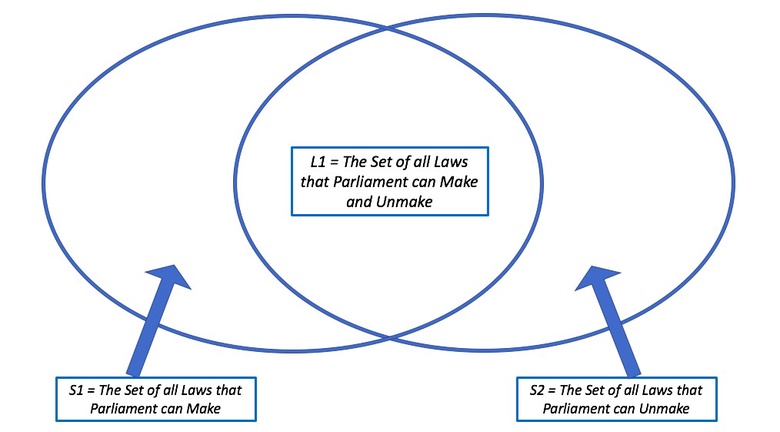
The positioning of L1 in this solution raises in turn the question of where the L2 category that I provided earlier should be situated in relation to these calculations. L2 is “The set of all laws that Parliament cannot make and unmake”. In the context of this more advanced S1/S2 reading, L2 is largely ambiguous and thus not helpful. The ambiguity arises from L2’s apparent capacity to cover what is not in both S1 and S2 simultaneously, and what is neither in S1 or in S2 individually. Thus, in this more sophisticated calculation, L2 as previously presented is not very helpful.



